ClutteredEnvPathOpt.jl Implementing Algorithms Efficiently in Julia
/mpolson64/ClutteredEnvPathOpt.jl
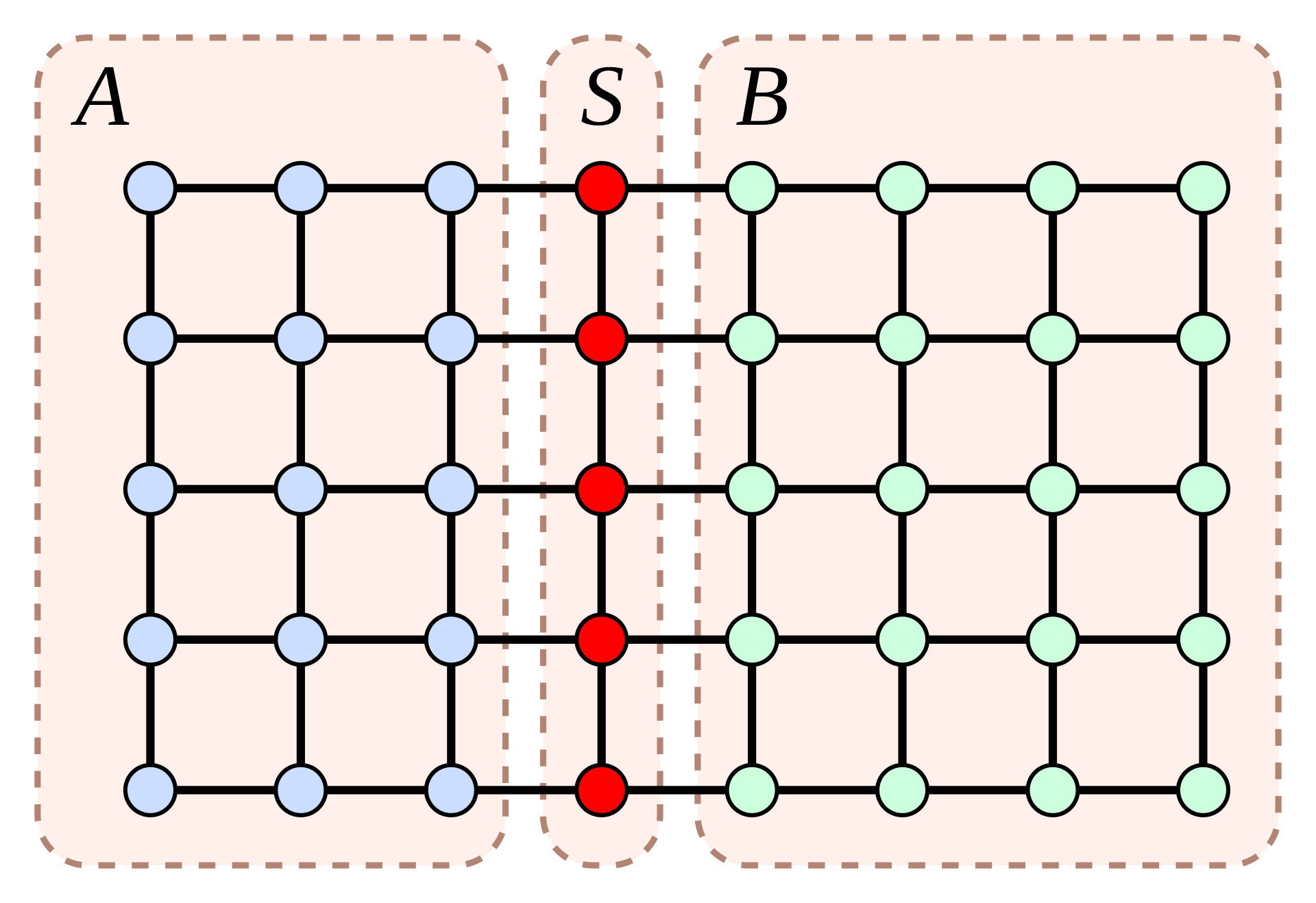
During my junior year at Rice University I worked as a research assistant for Joey Huchette on a project involving using Mixed Integer Programming to efficiently optimize quadcopter pathing through obstacle laden environments. The technique hinged on an innovative use of a divide-and-conquer style algorithm to calculate a biclique cover of a planar-like graph representing the environment and its obstacles. My responsibility was to implement this algorithm in Julia with speed and correctness as priority.
Much of my work centered on understanding the Lipton-Tarjan planar separator theorem. Using the theorem as a starting point I wrote a number of functions in Julia implementing its principles with slight variation and compared their real-world performance as the size of the input graph changed both in number of nodes and in number of edges. Our priority was to find a function that could quickly produce separations with balanced sides and small separators. Once I was satisfied with the performance, I modified the fastest function to operate on finite element graphs, the planar-like meshes our quadcopter routing problem would take as input. Finally, I implemented a divide-and-conquer style algorithm to find the biclique cover of a finite element graph a la mergesort, using the separator algorithm to partition the graph into progressively smaller pieces to recursively call the biclique cover calculating function on again.
So far, this project has been a great success and I hope we are able to publish soon. The task has been extremely interesting, and I was happy to have a chance to explore my passion for performance computing in a research setting. I am also happy this project gave me the opportunity to learn Julia, a language in which I had no prior experience but with which I am now very comfortable and productive.